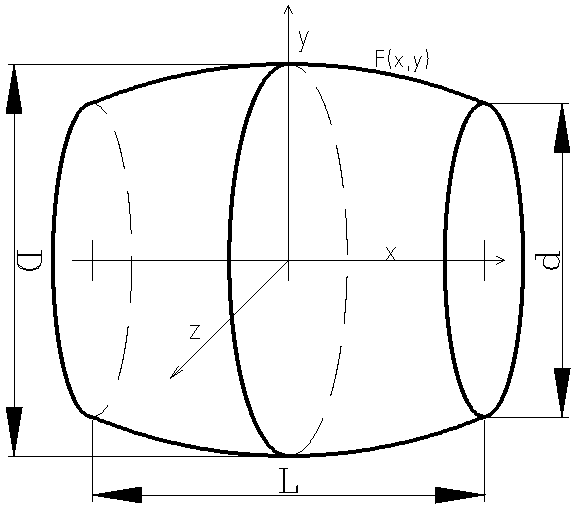
Jednoho dne mne soused zaskočil tvrzením, že dodnes není znám vzorec pro výpočet objemu normálního dřevěného sudu. Tak jsem pátral po Internetu a opravdu není lehké najít v češtině relevantní data. Nicméně tento problém je opravdu starý, počíná zřejmě už Archimedem ale první zmínka o relevantním vzorci je spojena se jménem matematika a hvězdáře Johanna Keplera. Kepler koupil sud vína na svatbu a způsob měření objemu obchodníka s vínem ho rozhněval. Poté studoval, jak vypočítat plochy a objemy těchto těles a napsal o tom knihu (vydanou v roce 1615): „Nova Stereometria doliorum vinariorum“, kde se uvádí i formule (vzorce, jak je známe dnes se tehdy ještě nepoužívaly) aproximující sud ořezaným rotačním elipsoidem. Tato formule se používá dodnes a je tedy už více jak čtyři století stará.
Po formulaci infinitezimálního počtu Newtonem a Leibnizem byly odvozeny další vzorce, aproximující plášť sudu jinými funkcemi, které by lépe odpovídaly realitě. Zde bude použita kromě původní eliptické ještě aproximace parabolická, čistě kruhovou, která se zdá nejlepší vynecháme - ne, že by to nešlo, ale výsledný vzorec je dost složitý a pro mírné zakřivení sudu není rozdíl mezi jednotlivými vzorci tak velký, aby se to nějak významně projevilo v praxi.
| Aproximace pláště | Eliptická (Kepler) | Parabolická |
| Funkce F(x,y) | $ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $ | $ y = ax^2 + b $ |
| Výsledný vzorec | $ V = \frac{L \pi}{12} \left(2 D^{2} + d^{2}\right) $ | $ V = \frac{L \pi}{60} \left(8 D^{2} + 4 D d + 3 d^{2}\right) $ |
Podrobnosti odvození jsou ve skriptu, který to umí symbolicky spočítat. Celkem nic na tom není - v aproximující funkci $ F(x,y) = 0 $, což je obecné vyjádření řezu sudem v rovině x,y, se parametry a,b vyjádří pomocí rozměrů d,D a pak se integruje element objemu $ dV = S dx, S = \pi y^2 $, tedy $ V = \pi \int_{-L/2}^{+L/2} y^2 dx $. Sud má rotační symetrii podle osy x, dále pak zrcadlovou symetrii podle roviny y,z. Z toho plyne, že pokud vyjádříme y = f(x), pak bude tato funkce vždy sudá. Pro aproximaci se tedy dá použít libovolný sudý polynom, ale třeba i funkce cos(x). I to se někdy používá v praxi, ale uvedené dva vzorce stačí, sud stejně nikdy nemá nějaký zcela přesný matematický tvar. Podstatné je, že používané aproximační funkce, resp. jejich kvadrát lze analyticky integrovat, tedy lze nalézt primitivní funkci v uzavřeném tvaru. Platí to i pro tu aproximaci kružnicí, jen zůstane pod integrálem druhá odmocnina a tím je dána ta složitost. Celou práci odvádí knihovna sympy, která umí nejen upravovat symbolické výrazy, ale i řešit rovnice, derivovat a integrovat. Ruční výpočet je více náchylný na zanesení chyby.