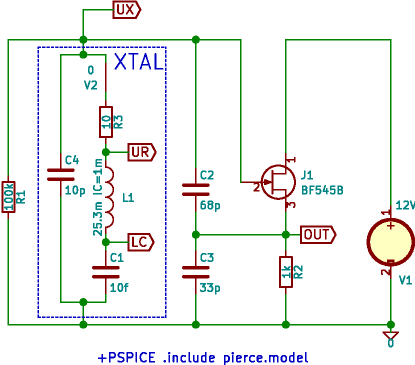
Obvyklé zapojení krystalového oscilátoru je tzv. Pierceovo. Takto obvykle fungují i oscilátory integrované v čipech, např. mikroprocesorech. Jen je tranzistor nahrazen hradlem, vazební kondenzátory v principu zůstávají.

Je funkční, jednoduché, ale krystal rezonuje v paralelním módu, kapacity C2, C3, parazitní kapacity JFET a ostatních součástek poněkud ovlivňují stabilitu kmitočtu. Vazba mezi zesilovačem a krystalem, určená poměrem C2/C3 je trochu těsná a to má opět vliv na požadovanou přesnost. Těsnější vazba se v praxi volí především kvůli tomu, že použité součástky mají určitý rozptyl parametrů a zapojení musí fungovat za jakýchkoli okolností. Budu se proto snažit
Pozn. Krystaly se vyrábějí hlavně pro paralelní rezonanci se zatěžovací kapacitou $ C_L $, přičemž vztah mezi paralelním a sériovým rezonančním kmitočtem je $ f_p \approx f_s \left( 1 + \frac {C_1}{ 2 C_L} \right) $. $ C_L $ zahrnuje všechny kapacity paralelně připojené ke krystalu, tedy parazitní i sériovou kombinaci C2, C3. Výrobce tuto kapacitu $ C_L $ pro nominální frekvenci kmitů definuje a podle ní se pak volí kapacity C2, C3. Kromě toho se vyrábějí i krystaly, které mají jako nominální frekvenci $ f_s $ (sériové) a na uživateli je aby tomu svou konstrukci přizpůsobil. O to se zde budu snažit, sériová rezonance by měla být stabilnější.
Předchozí zapojení je typicky zpětnovazební oscilátor. Kromě toho je možné sestrojit i oscilátory dvojpólové, kde jsou ztráty v reálném LC obvodu kompenzovány záporným diferenciálním odporem. Je to jednodušší pro matematické modelování a existují i praktické prvky, které záporný diferenciální odpor vykazují. Ve fyzice je harmonický oscilátor prakticky nejvíce používaný model chování systémů a je proto dost dobře prozkoumán. Mechanicky je takový systém lineární, platí zákon zachování energie - kinetická energie se mění na potenciální a naopak. Modelujeme tak třeba kuličku na pružině, kyvadlo a podobné systémy, kde je pohyb v potenciálové jámě kvadratického tvaru a platí rovnice pro Hamiltonián soustavy (v podstatě je to součet kinetické a potenciální energie)
\[ H(x,p) = \frac{p^2}{2m} + \frac{m \omega^2 x^2 }{2} \]
a z toho spočteme Hamiltonovy rovnice
\[ \dot x = \frac{\partial H}{\partial p} = \frac{p}{m} \quad , \quad \dot p = - \frac{\partial H}{\partial x} = - m \omega^2 x \]
kde x je souřadnice, p hybnost (Hamiltonovy zobecněné souřadnice), m hmotnost a $\omega$ kruhová frekvence kmitů (závisí na tuhosti, ale to není podstatné). Proč se tím zabývám - je vidět, že výrazy pro potenciální a kinetickou energii jsou principiálně stejné pro energii cívky a kondenzátoru, pokud zaměníme x,p za proud i a napětí u. Nebo obráceně - záleží na tom, zda je zapojení sériové nebo paralelní - Hamiltonián je pro obě souřadnice kvadratický. A to je to podstatné pro to aby oscilátor kmital harmonicky. Všechno, co je v rovnicích navíc tuto harmoničnost narušuje a právě to je důvod, proč hledáme řešení s co možná nejslabší vazbou na LC obvod. Řešení této jednoduché soustavy rovnic je známé v analytickém tvaru, ale až zavedeme nelinearitu, bude potřeba provést numerickou simulaci a pro ní je Hamiltonův formalizmus velmi vhodný.
Avšak pro elektrické obvody není nutné patlat se s celým Hamiltonovým formalizmem, stačí použít Kirchoffovy zákony - z předchozího povídání si vezmeme jen označení stavových proměnných. Pro základní obvod LC je pak (počítáme dále jako paralelní obvod) součet proudů do uzlu nulový $ i_L + i_C = 0 $. Pokud označíme $ i_L = v $ a napětí u, máme opět dvě diferenciální rovnice pro dvě neznámé (stavové proměnné) u,v :
\[ v + C \dot u = 0 \to \dot u = - \frac{v}{C} \]
\[ i_L = v \to \dot v = \frac{u}{L} \]
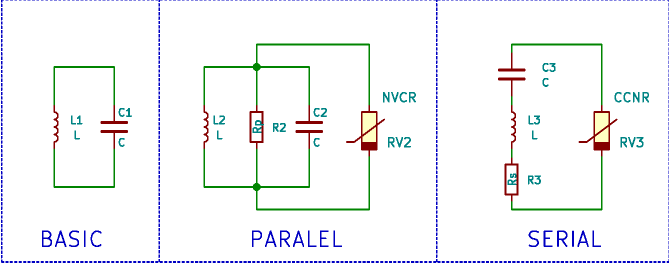
což je tvar vhodný pro numerickou simulaci. I když je analytický tvar řešení známý, je vhodné tyto rovnice použít a simulaci spustit. Zjistíme například, že nejjednodušší Eulerova metoda nevyhovuje - numerické řešení se rozejde se skutečností poměrně brzy. Pokud ale použijeme např. metodu Runge-Kutta 4. řádu, je řešení stabilní i pro poměrně velký krok metody. Že to není problém naprogramovat je vidět ze zdrojáků - žádná speciální knihovna není potřeba, je to jen pár řádek programu navíc. I když by ideální LC obvod takto harmonicky kmital do nekonečna, prakticky jsou v něm ztráty, které je třeba nějak kompenzovat. Použijeme nelineární prvek jehož charakteristika je typu N (levá strana obrázku, paralelní zapojení)
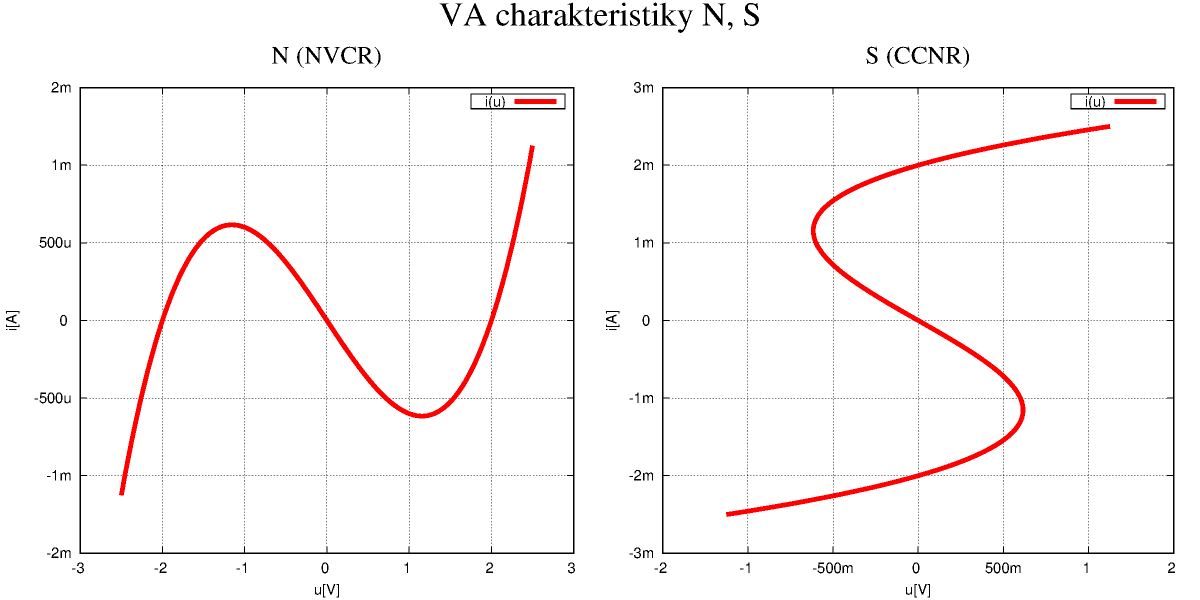
Tím se pomalu dostávám k jádru pudla. Obecné nelineární systémy mohou vykazovat dost podivné chování a jejich podrobná analýza je složitá. Zde můžeme zkusit, co to udělá, když pro kompenzaci ztrát použijeme negativní diferenciální odpor jehož voltampérovou charakteristiku aproximujeme polynomem 3. řádu $ i_{NVCR} = G u (u^2 - U_0^2) $. Lze si představit, že do tohoto výrazu je zahrnut i tlumící odpor $ R_p $ - změní se jen zvolené parametry simulace G a $ U_0 $. Budeme pak řešit nelineární diferenciální rovnice $ \dot u = - \frac {v + G u (u^2 - U_0^2)}{C} $ a $ \dot v = \frac{u}{L} $. Pokud je G relativně velké (těsná vazba), dostaneme pro fázovou trajektorii následující obrázek
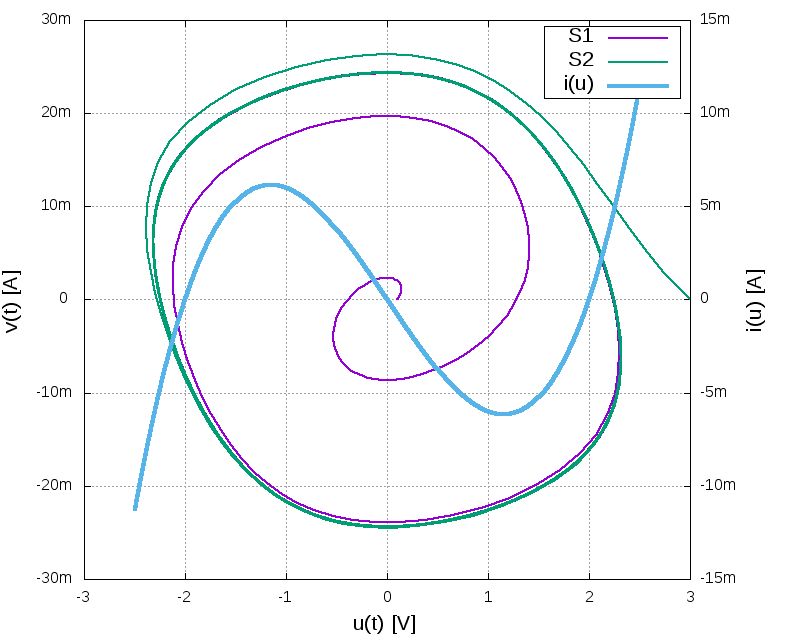
Co je z toho vidět :
Volná vazba (menší G) :
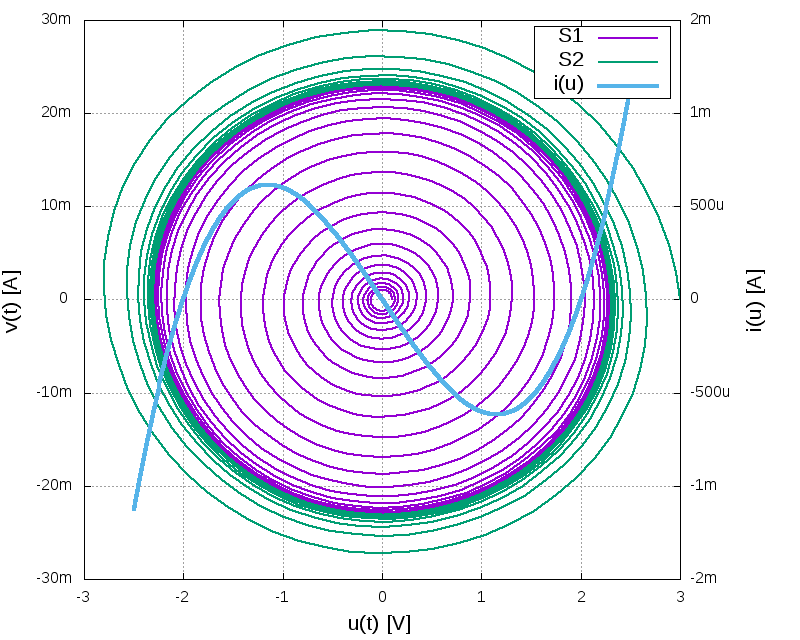
Ustálení trvá podstatně déle, avšak fázová trajektorie je už hodně podobná elipse.Volná vazba dává lepší fázovou trajektorii, i když je zde zapojen hodně nelineární prvek.
Celé předchozí povídání je dost divná teorie. Nakonec máme docela dobré simulátory elektrických obvodů, tak proč se patlat s nějakým Runge-Kutta. Jsou pro to docela dobré důvody
Pro paralelní zapojení LC a N charakteristiku záporného odporu je k dispozici několik prakticky možných řešení.
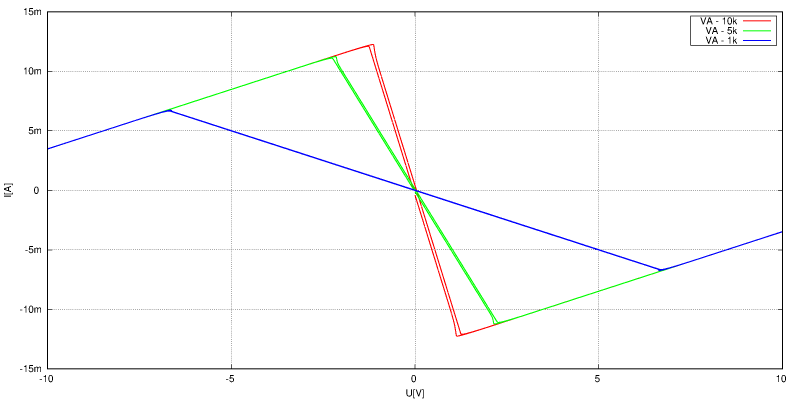
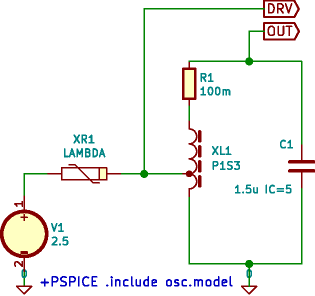
Pro sériové řešení (to co chci) jsem moc praktických zapojení nenašel. Existuje prvek UJT, který jde nasimulovat pomocí dvou tranzistorů, celé to pak poněkud připomíná náhradní zapojení tyristoru. Takže tyristor má v podstatě také S charakteristiku, ale není to použitelné, vazba by byla extrémě silná a nelze jí nijak řídit. Nicméně vhodné zapojení se najít dá
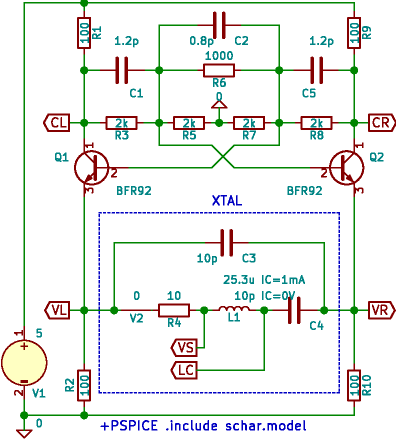
Toto zapojení vykazuje mezi body VL a VR přesně takovou charakteristiku CCNR, jaká je potřeba, přičemž strmost záporného odporu lze poměrně jednoduše řídit změnou jediného prvku - odporu R6.
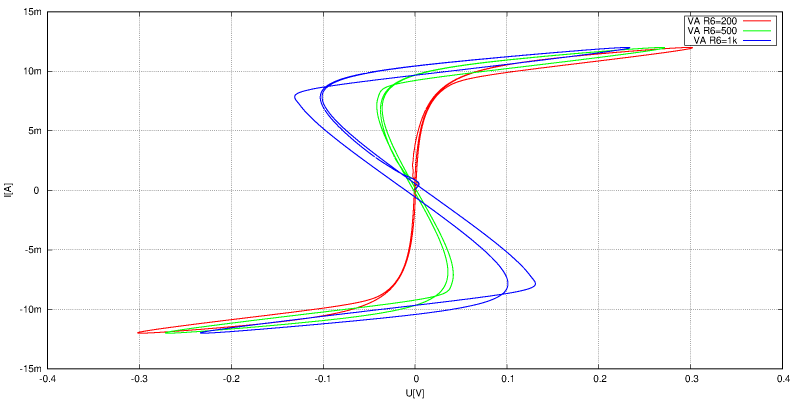
VA charakteristika je simulována při pracovní frekvenci 10 MHz, takže se už projevují dynamické jevy. Je k tomu potřeba udělat pár nezbytných poznámek
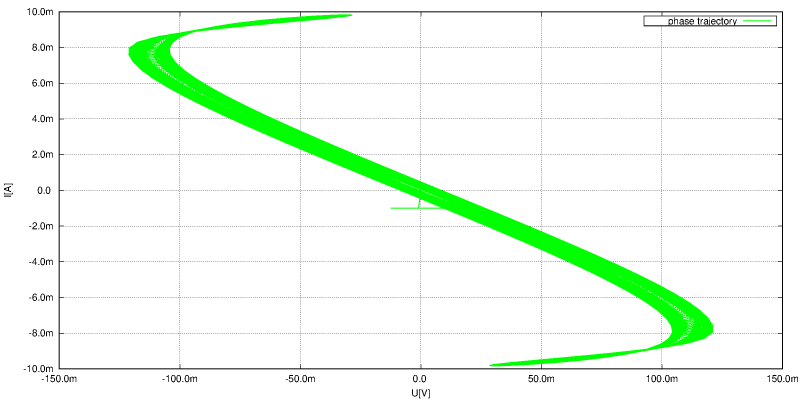
Trajektorie ve fázovém prostoru - napětí mezi VL a VR vs proud sériovým RLC. Je zčejmé, že takto volené souřadnice v podstatě kopírují VA charakteristiku zapojení. Pokud bych použil napětí na akumulačním prvku L nebo C vs. proud jím protékaný byla by to poměrně dokonalá elipsa.
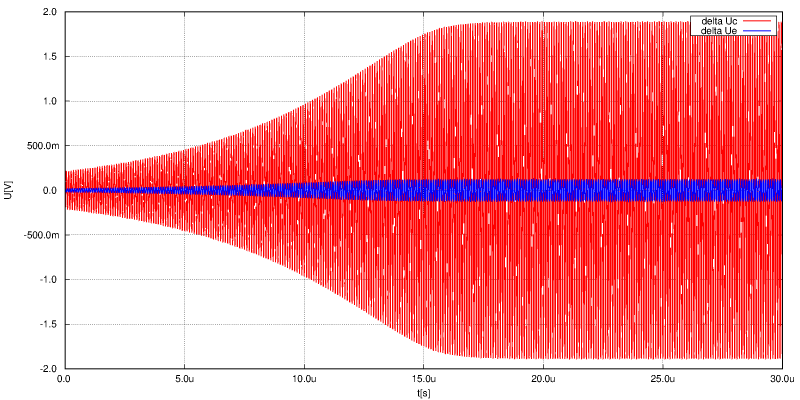
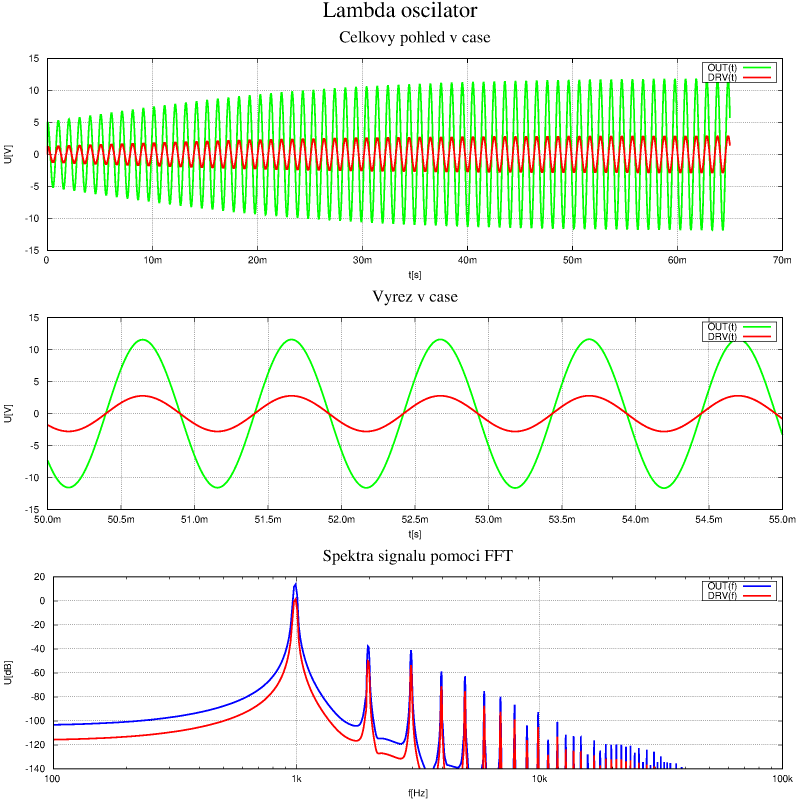
Časový průběh oscilací. Je zřejmé, že se to chová celkem rozumně, vazba zde je celkem volná. Zmenšení R6 na 500 $\Omega$ způsobí již postupný zánik oscilací, což ovšem může být způsobeno i omezenou přesností numerických výpočtů v simulátoru ngspice. Tyhle vlivy jsou už velmi jemné. Na místě R6 by bylo na místě použít trimr nebo lépe symetrický JFET řízený PI regulátorem na základě amplitudy kmitů. Poslední problém, který by byl potřeba vyřešit je přesné doladění kmitočtu krystalu. To by snad šlo i zde udělat varikapem nebo změnou teploty.
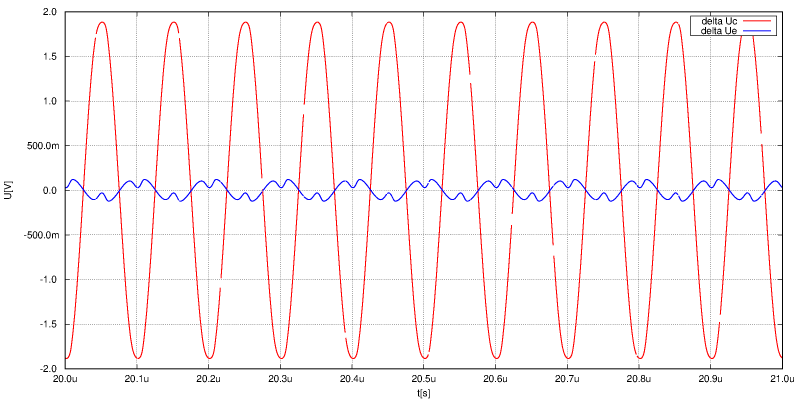
Pro představu i podrobnější výřez z předchozího obrázku. Na kolektorech je už znát zkreslení, zato rozkmit je dost velký. Proto by asi bylo dobré dodělat tu regulaci amplitudy.
Asi by nebyl problém postavit to zkusmo na bastldesce, ale nemám prostředky jak to otestovat - pro test kmitočtového normálu je potřeba o několik řádů lepší normál a ten nemám. A když si pořídím rubidiový normál, nebudu mít už důvod se tímto zabývat. Takže to zůstává zatím jen jako idea. Pro hraní přibalíme výchozí soubory a pro úplnost jsou potřeba i následující programy (běžné v prostředí Linuxu) :
Simulace elektronických obvodů je v Linuxu dost problém, přece jen ve Windows jsou sice relativně drahé, ale daleko lepší programy pro tento účel. Dříve jsem používal Qucs, ale je hodně omezený na předdefinovanou sadu součástek. Simulace se ne vždy podaří, někdy je nutné měnit některé parametry, které však nejsou dobře popsány. Kromě toho musím nakreslit schéma, které je mi pak už k ničemu pokud se rozhodnu obvod realizovat.
Schéma nakreslíme v eeschema. Důležité je pochopit formát souboru *.cir pro ngspice a jak do něj dostat potřebné parametry – příkladem budiž textové pole uvozené +PSPICE a divné hodnoty součástek jako sin(0 20 2k). +PSPICE uvozuje text, který je připojen na konec souboru *.cir, -PSPICE uvozuje text kopírovaný na začátek. Není tedy nutné ručně tento editovat – nakonec ruční editace tohoto souboru je nevhodná, protože je generován programem. Hodnoty součástek používá simulační program a tedy to lze najít v manuálu ngspice, který je jako ostatně většina podobných manuálů dost nepřehledný. Všimněme si, co provádí třeba jednoduchý soubor jfet/osc.model. Model pro LAMBDA, tedy spojení P a N JFET je uděláno ručně, stejně jako vázaná indukčnost P1S3. Podle manuálu se vezmou příslušné prvky, pospojují se dohromady a správně se namapují vnější vývody. Nic víc a nic míň, to je celý princip jak udělat model pro složitější obvod s daným rozložením vývodů. Přitom schéma lze dále použít i pro kreslení plošného spoje. Důležité je dodržovat pro reference prvků schématu správné prefixy – pro složené prvky musí být prefix X, což eeschema umí zařídit pro prvky s prefixem U a IC, pro ostatní si musíme dát pozor. V zásadě tedy lze používat prvky ze standardních knihoven a ty pak lehce přizpůsobit simulaci. Rozložení vývodů u tranzistorů zde není řešeno, pořadí vývodů ve schématu je tak, jak vyžaduje model – bylo by nutné pozměnit pořadí vývodů u pouzdra. Jiná možnost by byla použít standardní rozložení vývodů a pro simulaci toto přizpůsobit pomocí přidání [Spice_Node_Sequence] uživatelského pole a definovat sekvenci např. 2,1,0 – viz. poznámka v souboru *.cir. Netlist vytvoříme ve formátu Spice, tedy soubor se sufixem .cir se zaškrtnutými volbami „Default format“ a „Prefix references 'U' and 'IC' with 'X'“ (pokud je potřeba).
Další zpracování není provedeno bash skriptem, ale pomocí jednoduchého makefile. Výsledek dávám do obrázku pomocí gnuplot a řídících souborů *.cmd. Ono to působí hodně těžkopádně, ale s těmi výsledky lze dělat různá kouzla, chce to trochu cviku. Kompatibilní spice modely různých součástek lze bez problémů najít na webu. Ani není nutné používat gnuplot, ngspice v interaktivním režimu umožňuje dělat různé věci, chce to prostudovat manuál.